试论数学解题要素

试论数学解题要素

陈具才 周力平

本文发表于《甘肃教育》1995年04期

知网收录（北大核心）：

　　数学解题在建立和发展数学认知结构，形成和增进数学思惟能力，培养和造就创造性精神等方面起着重要的作用。然而，题海无边，如何解题，就成了一个永恒的研究课题。
要加强解题的知识因索
解题研究的一代宗师波利亚说过：“货源充足和组织良好的知识仓库是一个解题者的重要资本。”所以要想成为解题能手，没有什么灵丹妙药和通天捷径，最根本的就是要学好数学基础知识并掌握其体系。“欲致鱼者先通水，欲致鸟者先树木。”除了理解知识，加深记亿外，要搞清各种概念、公式、定理和原理的来龙去脉，透过数量关系的表面形式深刻理解它们内在的联系和本质属性。有了充实、丰富和系统的知识功底，数学能力就会得以发展和提高，高效正确的解题就有了深厚的基础。
张奠宙先生说得好：“解数学题的实质，就是意味着找出这样一个数学的一般原理（定义、公理、定理、法则、定律、公式）的序列，当应用它们到问题的条件或条件的推论（解法的中间结果）时，我们就得到问题所要求的答案。”那么，凭什么找出这个“序列”呢？
要掌握基本的数学思想和数学方法
光拥有解题的知识宝库是不够的，还要有打开宝库的钥匙和用宝的窍门，这就是数学思想和数学方法。数学思想是抽象概括的结题指导思想，它提示了思考和解决问题的基本方向，足一种宏观策略，有着广泛的应用。诸如函数与方程，化归与转化，演绎与归纳，数形结合，分类讨论，类比联想，以退求进，正难则反等思想。数学方法是更具体，更有燥作性的措施，在应用中显得直接而有效。常用的数学方法有综合法、分析法、待定系数法、配方法、数学归纳法、参数法、反证法、比较法，构造法、判别式法等。对于一个具体问题，则需要在这“一大串钥匙”中挑选适当的一把或几把，来帮助我们打开知识之门，寻求解题之路，建构解题之“序列”。
要有合理的解题程序
一遇到题目，不加思索或者对紊乱的思绪不作整理，就匆忙下手，急于求成，往往是欲速则不达，或者事倍而功半。有条不紊地思考分析问题是解题成功的关健。解题的一般程序如下。
1.审题。对这一步决不可掉以经心，要把题意理解准确，搞清目标；要把各个条件找全，化隐为显；要思考每个条件的作用，随时调用。否则就会造成解题失误。
2.分所判断，选择解法。通过审题，在收集、动员了题目中已知的信息之后，要对这些信息进行组合、整理和加工。先应进行联想，考查一下自己足否见过或解过类似的题目，可否沿用同一解法来解这道题或者作些适当的变换才可能。正如波利亚所建议的，“你是否知道与此有关的问题，你是否知道一个可以用得上的定理”，“看着未知数，试想出一个具有相同未知数或相似末知数的熟悉的问题”。这些尝试如不成功，则可看看问题的几何背景、特殊情形、反面情况等，也许由此预见解题思路。总之，需要在所有信息标示的蛛丝蚂迹中去探寻，或从目标所提供的“情报”中找到解题突破口；或从问题条件出发，紧盯目标，抓主要矛盾，顺藤摸瓜，重点突玻。
例如，1993年高考题，α、β是关于χ的方程χ²＋aχ＋b＝0的二实根，若|α|＜2，|β|＜2，求证：2|a|＜4＋b且|b|＜4。我们可作如下分析，结论是关于系数a，b的式子，而条件中有根α、β，这就使我们想到用韦达定理变结论为2|α＋β|＜4＋αβ,且|αβ|＜4。后者显然成立，欲证前者，注意到α、β同在一式里，而条件中的α、β是分离的，故可作出反应：分解结论。又如何处置绝对值呢？对策有二：或转化为－4－αβ＜2(α＋β)＜4＋αβ（即(α＋2)(β＋2)＞0且(α－2)(β－2)＞0)，或考虑平方差(4＋αβ)²－[2(α＋β)]²＝(4－α²)(4－β²)＞0，至此，条件与结论之同的“大山隧道”己经打通，找到了证明思路。
诚然，我们在探寻解题途径时，常会一筹莫展，束手无策。这时，我们不应去走死路一条，而要及时果敢地进行思维转换，另辟蹊径，有时通过严谨的逻辑思维或常规的分析方法，也可能产生顿悟或灵感，思维瞬间闪光。
例如，1985年高考题：设A＝{(x，y)|x＝n，y＝an＋b，n∈Z，a、b∈R}，B＝{(x，y)|x＝m，y＝3m²＋15，m∈Z}，C＝{(x，y)|x²＋y²≤144，x、y∈R}，问是否存在a与b，使(1)A∩B≠∅，(2)(a，b)∈C同时成立？这是一道探索性半开放问题，假设存在满足(1)(2)的a、b，则有n∈Z使an＋b＝3n²＋15与a²＋b²≤144同时成立。欲从参数最多的an＋b处着手突破（一反常规，整体考虑，用几何意义或关于a、b的代数混合组是否有解去研究），但又无法下手，迷茫之际，发现3n²＋15与a²＋b²中与a、b“各自为阵”，柯西不等式正具有这种分离作用。便有3n²＋15＝an＋b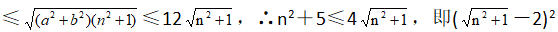≤0，∴n²＝3，这与n∈Z矛盾。故不存在符合条件的a和b。这个解法奇巧简捷，别出心裁，出奇制胜。
3.实施解题。（略）
4.检验反思。解题过程书写完毕后，不应置诸高阁，要在刚刚完成任务，而且自己的体验还在头脑中保持着新鲜之感的时候，恰如其分地去回顾自己刚才的所作所为，将大大有利于探索自己刚才克服困难的关键之处，还可以有目的地对自己提出许多有益的问题。如：关键在哪里？什么地方还可以完成得更好些？我为什么没有觉察到这一点？要看出这一点必须具备哪些知识？应该从什么角度去考虑？这里有没有值得学习的诀窍可供以后遇到类似问题时应用？（波利亚语）只要坚持不懈地如此反思，何愁能力不会提高。
要积累解题经验，探索解题捷径
一个题目的解法往往不止一种，但比较这些解法，却有繁简与优劣之分，这就需要我们在解题实践中注意积累经验，探索规律，不断总结，从而有所发现、有所提高。要勤思精练，在形式不同的众多题目中，注意选取性质相近、思路相仿、方法类同的题目，进行合理归纳，分类整理，发现联系，总结特征，掌握基本题型的技能技巧，举一反三，触类旁通，这是提高解题效率的有效途径。